细粉加工设备(20-400目)
我公司自主研发的MTW欧版磨、LM立式磨等细粉加工设备，拥有多项国家专利，能够将石灰石、方解石、碳酸钙、重晶石、石膏、膨润土等物料研磨至20-400目，是您在电厂脱硫、煤粉制备、重钙加工等工业制粉领域的得力助手。
超细粉加工设备(400-3250目)
LUM超细立磨、MW环辊微粉磨吸收现代工业磨粉技术，专注于400-3250目范围内超细粉磨加工，细度可调可控，突破超细粉加工产能瓶颈，是超细粉加工领域粉磨装备的良好选择。
粗粉加工设备(0-3MM)
兼具磨粉机和破碎机性能优势，产量高、破碎比大、成品率高，在粗粉加工方面成绩斐然。
CE平分角ACD
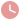
如图：在 ABC中，CE平分∠ACB，CF平分∠ACD，且EF∥BC
根据角平分线的定义可以证明出 CEF是直角三角形，再根据平行线的性质以及角平分线的定义证明得到EM=CM=MF然后求出EF的长度，然后利用勾股定理列式计算即可求解． 结果二 题目 如图，在 ABC中，CE平分∠ACB,CF平分∠ACD,且EF‖BC交AC于M,若CM＝5， 如图，在 ABC中，CE平分∠如图,∠ACD是 ABC的外角,BE平分∠ABC,CE平分∠ACD,且BE,CE交于点E试说明：∠E=1/2∠A 角ACD是三角形ABC的一个外角,角ABC和角ACD的平分线BE,CE交于点E,则角A与角E有什么样 如图：∠ACD是 ABC的外角，BE平分∠ABC，CE平分∠ACD 2011年9月10日 如图，在 ABC中，CE平分∠ACB,CF平分∠ACD,且EF‖BC交AC于M,若CM＝5，则CE^2+CF^2=?解：∵CE平分∠ACB，CF平分∠ACD，∴∠ACE= ∠ACB，∠ACF= 如图，在 ABC中，CE平分∠ACB,CF平分∠ACD,且EF‖BC交AC于M,
如图1，CE平分∠ ACD，AE平分∠ BAC，∠ EAC+∠ ACE=90
解析 (1)AB ∥ CD；理由如下： ∵ CE平分∠ ACD，AE平分∠ BAC， ∴ ∠ BAC=2∠ EAC，∠ ACD=2∠ ACE， ∵ ∠ EAC+∠ ACE=90°， ∴ ∠ BAC+∠ ACD=180°， ∴ AB ∥ CD； (2)∠ 如图，在 ABC中，CE平分∠ ACB，CF平分 ABC的外角∠ ACD，且∠ ACD交AC于M，若CM=4，则CE^2+CF^2的值为（ ） $\because CE$平分$\angle ACB$，$CF$平分$\angle 如图，在 ABC中，CE平分∠ ACB，CF平分 ABC的外角∠ 2011年6月11日 考点：角平分线的性质．专题：证明题．分析：如图过点E分别作EG⊥BD、EF⊥BA、EI⊥AC，垂足分别为G、H、I，根据角平分线的性质可得EF=EG，EI=EG，再根据 如图，已知BE平分∠ABC，CE平分∠ACD,且交BE于E。求证：AE平分∠2010年9月23日 关注 证明：过E点作：EF垂直于BD于F，EG垂直于AC于G，EH垂直于BM于H， 则；BE平分∠ABC，有EF=EH， CE平分∠ACD，EG=EF， 则：EH=EG， 所以：AE平 如图，已知BE平分∠ABC，CE平分∠ACD，且交BE于点E，求证AE平分∠
如图，已知BE平分∠ABC，CE平分∠ACD，且交BE于E
如图过点E分别作EG⊥BD、EH⊥BA、EI⊥AC，垂足分别为G、H、I，根据角平分线的性质可得EH=EG，EI=EG，再根据角平分线的性质的逆定理可证AE平分∠FAC． 本题考点： 角平分线 答案 H E B C DE分别作EG⊥BD、EH⊥BA、EI⊥AC，垂足分别为G、H、I，∵BE平分∠ABC，EG⊥BD，EH⊥BA，∴EH=EG∵CE平分∠ACD，EG⊥BD，EI⊥AC，∴EI=EG，∴EI=EH 61、如图，已知BE平分∠ABC，CE平分∠ACD，且交BE于E 在 ACE中，∠BAC=∠E+∠2=∠E+∠B+∠E=∠B+2∠E， 即：∠BAC=∠B+2∠E． 根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠1，根据角平分线的定义可得∠1=∠2，再次利用三 如图，CE是 ABC的外角∠ACD的角平分线，且CE交BA的 2011年9月10日 则CE^2+CF^2=?解：∵CE平分∠ACB，CF平分∠ACD，∴∠ACE= ∠ACB，∠ACF= ∠ACD，即∠ECF= （∠ACB+∠ACD）=90°，又∵EF∥BC，CE平分∠ACB，CF 百度首页 商城 注册 登录 资讯 视频 图片 知道 文库 贴吧 采购 地图 更多 答案 我要 如图，在 ABC中，CE平分∠ACB,CF平分∠ACD,且EF‖BC交
如图，在 ABC中，CE平分∠ ACB，CF平分 ABC的外角∠
如图，在 ABC中，CE平分∠ ACB，CF平分 ABC的外角∠ ACD，且∠ ACD交AC于M，若CM=4，则CE^2+CF^2的值为（ ）A8B16C3 【解析】because CE平分angle ACBtherefore angle ACE=angle BCE=dfrac{1}{2}angle ACBbecause CF平分angle ACDtherefore [答案]75°[解析][分析]如图过点E分别作EG⊥BD、EH⊥BA、EI⊥AC,垂足分别为G、H、I,根据角平分线的性质可得EH=EG,EI=EG,再根据角平分线的性质的逆定理可证AE平分∠FAC,再根据∠FAC与∠BAC互补即可[详解]证明:如图所示:过点E分别作EG⊥BD、EH⊥BA、EI 61、如图，已知BE平分∠ABC，CE平分∠ACD，且交BE于E [答案]90°[解析]试题解析:AB∥CD,∠BAC+∠ACD=180°，∵AE平分∠BAC,CE平分∠ACD,Z1=∠BAC,2∠ACD, 2Z1+∠2=（∠BAC+LACD)x180°=90 2 2故答案为90点睛:两直线平行,同旁内角互补如图：AB∥CD，AE平分∠BAC,CE平分∠ACD，则∠1＋∠2 如图1：已知直线AB∥CD，∠ACB=∠ABC，CE平分∠ACD．（1）求∠BCE的度数；（2）如图2，点F是线段AB上一点，连接CF，且∠BCF=∠DCE．①求证：CF平分∠ECM；②如图3，点N是线段CF上一点，且∠NAF+2∠FCM=180°，点H是线段AC上一点且∠HNA 如图1：已知直线AB∥CD，∠ACB=∠ABC，CE平分∠ACD
如图，已知BE平分∠ABC，CE平分∠ACD,且交BE于E。求证
2011年6月11日 如图，已知BE平分∠ABC，CE平分∠ACD,且交BE于E。求证：AE平分∠FAC过点E作EM EN EO分别垂直于BD AC BF垂足为M N O 因为BE平分∠ABC 所以EM=EO（角平分线上的点到角两边的距离相等） 同理EM=EN 所以EO=EN 所以AE 过E作EF⊥DC于F,根据正方形的性质和角平分线的性质以及勾股定理即可求出DE的长 本题考查了正方形的性质:对角线相等,互相垂直平分,并且每条对角线平分一组对角、角平分线的性质:角的平分线上的点到角的两边的距离相等以及勾股定理的运用如图，已知正方形ABCD边长为1，连接AC、BD，CE平分∠ 2015年3月11日 因为角BAC＋角ACD＝180度 又因为CE平分角ACD,AE平分角BAC 角1＝二分之一角BAC 角2＝二分之一的ACD 所以角1＋角2＝90度如图，已知CE平分∠ACD，AE平分∠BAC，且AB∥CD，试 2010年9月23日 ∵CE平分∠ACD，EG⊥BD，EI⊥AC ，∴EI=EG，∴EI=EH（等量代换），∴AE平分∠FAC（到角两边距离相等的点一定在角的平分线上）． 点评：本题主要考查角平分线的性质及其逆定理；准确作出辅助线是解答本题的关键 如图，已知BE平分∠ABC，CE平分∠ACD，且交BE于点E
如图1，CE平分∠ ACD，AE平分∠ BAC，∠ EAC+∠ ACE=90
如图1，CE平分∠ ACD，AE平分∠ BAC，∠ EAC+∠ ACE=90°(1)请判断AB与CD的位置关系，并说明理由；(2)如图2，在（1）的结论下，当∠ E=9 ∴∠BAC=∠PQC+∠QPC 本题考查了平行线的判定和性质,性质由形到数,用于推导角的关系并计算,常常构造平行来进行 2015年9月15日 如图，BE平分∠ACD，CE平分外角∠ACD,若∠A=42° 如图，∠ACD是 ABC的外角，∠A=40°，BE平分∠AB 更多类似问题 > 为你推荐： 特别推荐 “网络厕所”会造成什么影响？ 华强北的二手是否靠谱？ 新生报道需要注意什么？ 如图，BE平分角ABC,CE平分角ACD，求证：角E＝二分之一 2016年1月28日 CE平分∠ACD，∠A=110°，则∠ECD等于度∵AB ∥ CD，∴∠A+∠ACD=180°，∵∠A=110°，∴∠ACD=70°，∵CE平分∠ACD，∴∠ECD= 1 2 ∠ACD=35°，故答案为：35 ． 已知：如图AB ∥ CD，CE平分∠ACD，∠A=110°，则∠ECD 2016年12月1日 如图，已知BE平分∠ABC，CE平分∠ACD，且交BE于E。求证：AE平分∠FAC。 展开 我来答 1个回答 #合辑# 面试问优缺点怎么回答最加分？ 沫晓忆194 推荐于 TA获得超过143个赞 知道答主 回答量： 156 采纳率： 57% 帮助的人 如图，已知BE平分∠ABC，CE平分∠ACD，且交BE于E
【题目】 请将下列证明过程补充完整： 已知：如图， AE 平分
【题目】 请将下列证明过程补充完整： 已知：如图， AE 平分∠ BAC ， CE 平分∠ ACD , 且∠ α ＋∠ 角平分线的定义,2∠β,等式性质,180°,等量代换,同旁内角互补,两直线平行[解析][分析]先根据角平分线的定义,得到∠ACD+∠BAC=2∠α+2∠β,再根据∠α+∠β=90°,即可得到∠ACD+∠BAC=180°,进而判定AB∥CD[详解 2017年5月17日 如图1，CE平分∠ACD，AE平分∠BAC，∠EAC+∠ACE=90°（1）求证：AB∥CD；（2）如图2，由三角形内角和可知∠E=90°，移动直角顶点E，使∠MCE=∠ECD，当直角顶点E点移动时，问∠BAE与∠MCD否存在确定的数量关系？如图1，CE平分∠ACD，AE平分∠BAC，∠EAC+∠ACE=90 如图,CE是 ABC的外角∠ACD的平分线,且CE交BA的延长线于点E(1)若∠B=35°,∠E=25°,求∠BAC的度数;(2)证明:∠BAC=∠B+2∠E 百度试题 结果1如图,CE是 ABC的外角∠ACD的平分线,且CE交BA的延长线于 (2)连MC,求证:MC平分∠BMD 相关知识点： 全等三角形 全等三角形的基本应用 全等形 全等形的概念及性质 全等形的性质应用 全等三角形的判定——基础 一般三角形全等的判定 AAS判定全等 全等的判定应用 多解或多种判定混合如图,CA=CD,CB=CE,∠ACD=∠BCE,AB与DE交于点M
请将下列证明过程补充完整:已知:如图,点E在AB上,且CE平分
[解答]证明:∵CE平分∠ACD∴∠2=∠ECD(角平分线的定义),∵∠1=∠2(已知)∴∠1=∠ECD(等量代换))∴AB∥CD(内错角相等两直线平行)故答案为:2,ECD,角平分线的定义,ECD,等量代换,内错角相等两直线平行2012年1月21日 如图，已知AE,CE分别是∠BAC,∠ACD的平分线，且∠1+∠2=∠AEC (1)试确定直线AB，CD的位置关系；（1）因为三角形AEC的内角和等于180度，所以角1+角2+角AEC=180度，因为角1+角2=2角AEC,，所以角1+角2=90度，因为AE 平分 百度首页 如图，已知AE,CE分别是∠BAC,∠ACD的平分线，且∠1+∠2 2015年8月10日 问： 如图，角ACD是三角形ABC的外角，BE平分角ABC，CE平分角ACD，且BE、CE交点于点E，求证：角E等于二分之一角A 展开 我来答 2个回答 #热议# 在购买新能源车时，要注意哪些？ 匿名用户 展开全部 证明： ∵∠ACD=∠A+∠ABC，∴∠ 问： 如图，角ACD是三角形ABC的外角，BE平分角ABC，CE 如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°B AB AM EE DC D图1图2(1)请判断AB与CD的位置关系并说明理由;(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的 答案 【题文】如图1，CE平分∠ACD，AE平分∠BAC，∠EAC+
（1）求证： ABE～ ACD； Baidu Education
分析:(1)先证 ABE∽ ACD,得出AE AB AD AC,再利用∠A是公共角,即可求证;(2)在BC上截取BF=BD,连接EF,先证 BDE≌ BFE,得出DE=FE,∠BDE=∠BFE,再证EF=EC即可解:(1)∵∠ABE =∠ACD,且∠A是公共角,∴ ABE∽ ACD∴AE AB AD AC,即AE AD AB AC,又∵ 解:∵∠BAC=∠ACD=90°,且∠ABC=∠ADC∴AB∥CD且∠ACB=∠CAD∴BC∥AD∴四边形ABCD是平行四边形∴答案①正确;∵∠ACE+∠ECD=∠D+∠ECD=90°∴∠ACE=∠D而∠D=∠ABC∴∠ACE=∠D=∠ABC∴答案②正确;又∵∠CEF+∠CBF=90°,∠AFB+∠ABF=90°且∠ABF=∠ 如图，∠BAC=∠ACD=90∘，∠ABC=∠ADC，CE⊥AD，且BE 2014年8月25日 如图，已知 ABC为等边三角形，D为BC延长线上的一点，CE平分∠ACD，CE=BD，求证： ADE为等边三角形证明：∵ ABC为等边三角形，∴ 如图，已知 ABC为等边三角形，D为BC延长线上的一点，CE 2013年4月27日 (1)求证：ACD ≌BCE ；1、CD平分∠ACE，所以∠1=∠2;CE平分∠BCD,所以∠2=∠3;所以∠1=∠2=∠3C是线段AB的中点，AC=CB,已知CD=CE，由边角边得 ACD≌ 百度首页如图，C是线段AB的中点，CD平分∠ACE，CE平分∠BCD
如图:∠ACD是 ABC的外角,BE平分∠ABC,CE平分∠ACD,且
2013年6月20日 如图:∠ACD是 ABC的外角,BE平分∠ABC,CE平分∠ACD,且∠BE、CE交于点E。求证：∠E=1/2∠A。 我来答2014年10月8日 （∠ACB+∠ACD）=90°，又∵EF∥BC，CE平分∠ACB，CF平分∠ACD，∴∠ECB=∠MEC=∠ECM，∠DCF=∠CFM=∠MCF，∴CM=EM=MF=5，EF=10，由勾股定理可知CE 2 +CF 2 =EF 2 =100．如图：在 ABC中，CE平分∠ACB，CF平分∠ACD，且EF∥BC 如图,CA=CD,CB=CE,∠ACD=∠BCE,AB与DE交于点M(1)求证:AB=DE;(2)连MC,求证:MC平分∠BMD 百度试题 结果1 结果2 题目 如图,CA=CD,CB=CE,∠ACD=∠BCE,AB与DE交于点M 如图,CA=CD,CB=CE,∠ACD=∠BCE,AB与DE交于点M 【题目】如图在 ABC中，BO，CO分别平分∠ABC，∠ACB，交于O，CE为外角∠ACD的平分线，交BO的延长线于点E，记∠BAC=∠1∠BEC=∠2,则以下结论①∠1=2∠2，②∠BOC=3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2,正确的是(把所有正确的结论的序 如图在 ABC中，BO，CO分别平分∠ABC，∠ACB，交于O
已知:如图,CE平分∠ACD,∠1=∠B,求证:AB∥CE Baidu Education
【解答】证明：∵CE平分∠ACD，∴∠1=∠2，∵∠1=∠B，∴∠2=∠B，∴AB∥CE．【分析】由CE为角平分线，利用角平分线的定义得到一对角相等，再由已知一对角相等，利用等量代换得到一对同位角相等，利用同位角相等两直线平行即可得证．2011年9月10日 则CE^2+CF^2=?解：∵CE平分∠ACB，CF平分∠ACD，∴∠ACE= ∠ACB，∠ACF= ∠ACD，即∠ECF= （∠ACB+∠ACD）=90°，又∵EF∥BC，CE平分∠ACB，CF 百度首页 商城 注册 登录 资讯 视频 图片 知道 文库 贴吧 采购 地图 更多 答案 我要 如图，在 ABC中，CE平分∠ACB,CF平分∠ACD,且EF‖BC交 如图，在 ABC中，CE平分∠ ACB，CF平分 ABC的外角∠ ACD，且∠ ACD交AC于M，若CM=4，则CE^2+CF^2的值为（ ）A8B16C3 【解析】because CE平分angle ACBtherefore angle ACE=angle BCE=dfrac{1}{2}angle ACBbecause CF平分angle ACDtherefore 如图，在 ABC中，CE平分∠ ACB，CF平分 ABC的外角∠ [答案]75°[解析][分析]如图过点E分别作EG⊥BD、EH⊥BA、EI⊥AC,垂足分别为G、H、I,根据角平分线的性质可得EH=EG,EI=EG,再根据角平分线的性质的逆定理可证AE平分∠FAC,再根据∠FAC与∠BAC互补即可[详解]证明:如图所示:过点E分别作EG⊥BD、EH⊥BA、EI 61、如图，已知BE平分∠ABC，CE平分∠ACD，且交BE于E
如图：AB∥CD，AE平分∠BAC,CE平分∠ACD，则∠1＋∠2
[答案]90°[解析]试题解析:AB∥CD,∠BAC+∠ACD=180°，∵AE平分∠BAC,CE平分∠ACD,Z1=∠BAC,2∠ACD, 2Z1+∠2=（∠BAC+LACD)x180°=90 2 2故答案为90点睛:两直线平行,同旁内角互补如图1：已知直线AB∥CD，∠ACB=∠ABC，CE平分∠ACD．（1）求∠BCE的度数；（2）如图2，点F是线段AB上一点，连接CF，且∠BCF=∠DCE．①求证：CF平分∠ECM；②如图3，点N是线段CF上一点，且∠NAF+2∠FCM=180°，点H是线段AC上一点且∠HNA 如图1：已知直线AB∥CD，∠ACB=∠ABC，CE平分∠ACD 2011年6月11日 如图，已知BE平分∠ABC，CE平分∠ACD,且交BE于E。求证：AE平分∠FAC过点E作EM EN EO分别垂直于BD AC BF垂足为M N O 因为BE平分∠ABC 所以EM=EO（角平分线上的点到角两边的距离相等） 同理EM=EN 所以EO=EN 所以AE 如图，已知BE平分∠ABC，CE平分∠ACD,且交BE于E。求证 过E作EF⊥DC于F,根据正方形的性质和角平分线的性质以及勾股定理即可求出DE的长 本题考查了正方形的性质:对角线相等,互相垂直平分,并且每条对角线平分一组对角、角平分线的性质:角的平分线上的点到角的两边的距离相等以及勾股定理的运用如图，已知正方形ABCD边长为1，连接AC、BD，CE平分∠
如图，已知CE平分∠ACD，AE平分∠BAC，且AB∥CD，试
2015年3月11日 因为角BAC＋角ACD＝180度 又因为CE平分角ACD,AE平分角BAC 角1＝二分之一角BAC 角2＝二分之一的ACD 所以角1＋角2＝90度2010年9月23日 ∵CE平分∠ACD，EG⊥BD，EI⊥AC ，∴EI=EG，∴EI=EH（等量代换），∴AE平分∠FAC（到角两边距离相等的点一定在角的平分线上）． 点评：本题主要考查角平分线的性质及其逆定理；准确作出辅助线是解答本题的关键 如图，已知BE平分∠ABC，CE平分∠ACD，且交BE于点E 如图1，CE平分∠ ACD，AE平分∠ BAC，∠ EAC+∠ ACE=90°(1)请判断AB与CD的位置关系，并说明理由；(2)如图2，在（1）的结论下，当∠ E=9 ∴∠BAC=∠PQC+∠QPC 本题考查了平行线的判定和性质,性质由形到数,用于推导角的关系并计算,常常构造平行来进行 如图1，CE平分∠ ACD，AE平分∠ BAC，∠ EAC+∠ ACE=90
消防沙硬化板结
--雷蒙磨轴承油道不通怎么回事
--淮安加气砖
--600600白云石工业磨粉机
--日产2800方火山岩生石灰雷蒙磨
--抹灰石灰石质量要求
--生石灰矿用建设需办什么设备
--矿石磨粉机生石灰
--电石泥矿磨机
--磨325目石灰石粉深加工设备结构
--立式磨矿石磨粉机PFY价格
--进口威猛粉碎机,单轴机磨辊
--双碱法脱硫设备价格
--粉碎机是什么样的
--水泥设备滚压机
--时产200吨无烟煤粉碎机
--路路通磨粉设备
--求购石场磨粉机
--小型粉碎机械案例
--上海生石灰购
--石灰石铄垫层多少钱一立方米
--生石灰石灰石生产线安装
--张家口市煤机厂归省里什么部门管
--辽宁本溪市方解石高压磨粉机什么牌子好
--福建莆田市白云石磨粉机加工细度
--虎路峪方解石厂
--硅石硅灰石回收设备硅石硅灰石回收设备硅石硅灰石回收设备
--高岭土做凝胶用
--新疆巴音郭楞蒙古方解石摆式磨粉机厂家报价
--筛煤高细立磨
--